Interpreting Multi-objective Evolutionary Algorithms via
Sokoban Level Generation

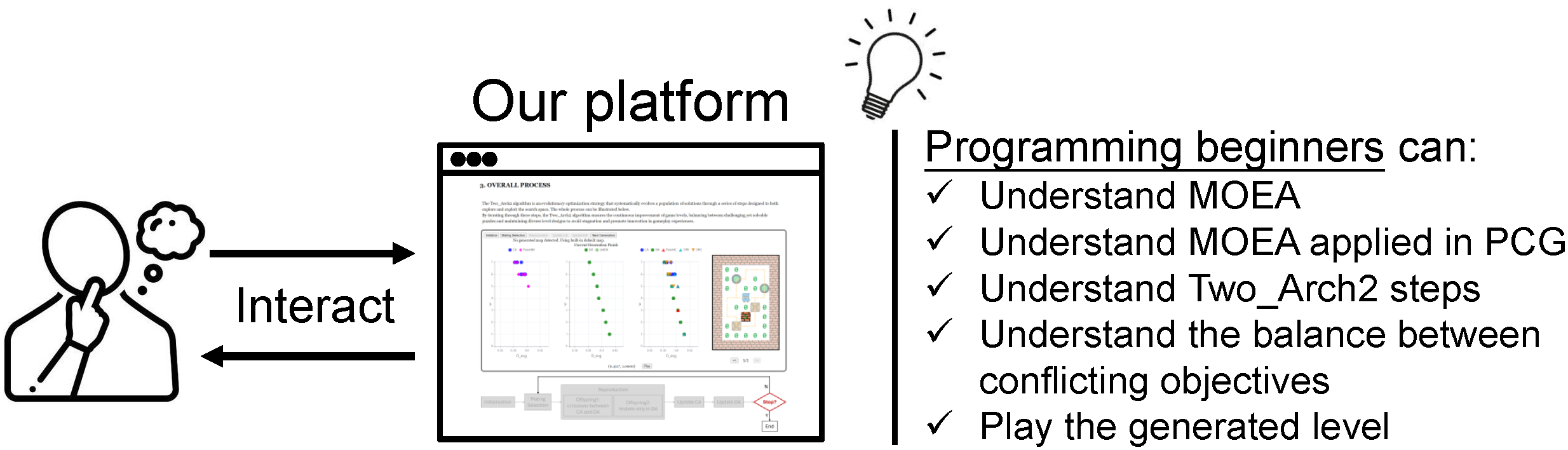
1. Introduction

In this section, we introduce the concept of MOPs, detail the application of MOEAs like Two_Arch2 for solving this kind of problem, and discuss the application in PCG.

1.1 Multi-objective Optimization Problem

In real life, we often encounter problems that involve conflicting objectives. These are known as multi-objective optimization problems (MOPs) [1]. An MOP can be defined as follows:

\(maximize\) \( f(x) = \{f_1(x),\dots, f_m(x)\}\).

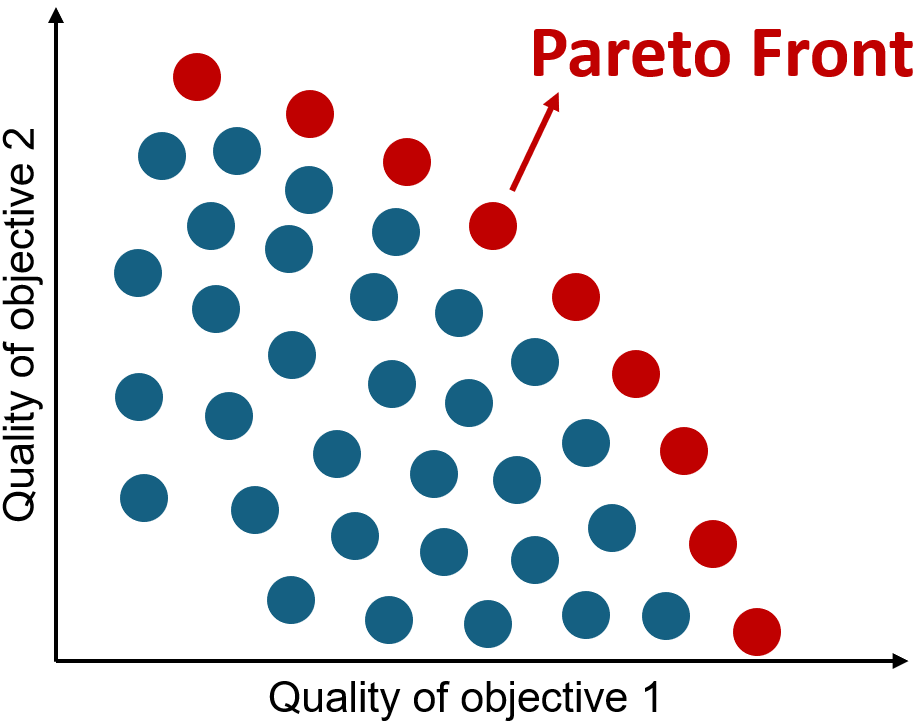
Here, \(x\) represents a solution within the decision space. The function \(f(x)\), comprising $m$ objectives, evaluates this solution. Each \(f_i(x)\) is an individual objective, where \(i\) ranges from 1 to $m$. A solution \(x\) is considered dominated to another solution \(x'\) if it is at least as good across all objectives, and better in at least one. Within a given set of solutions \(P\), those that aren’t outperformed by others form the non-dominated solution set. Unlike single-objective optimization where the goal is finding oen best solution, multi-objective optimization seeks a Pareto-optimal set, which includes all non-dominated solutions across the entire decision space. Each solution in this set represents a balance among the $m$ objectives. The effectiveness of the Pareto set approximation is typically assessed based on four criteria: convergence, spread, uniformity, and cardinality, with diversity considering both spread and uniformity [2].

The Pareto Front is a graphical representation that shows the trade-offs between the different objectives. Solutions on the Pareto Front are those that are not dominated by any other solutions, meaning no other solutions are better in all objectives. The Pareto Front helps in visualizing the efficiency of solutions where improving one objective would require compromising another, as shown below.

1.2 Multi-objective Evolutionary Algorithm

Multi-objective evolutionary algorithms (MOEAs) are techniques designed to tackle complex MOPs effectively. These algorithms use a population-based approach, optimizing over generations to approach the Pareto set based on the principle of survival of the fittest. Each solution, referred to as an individual, has a fitness level indicating its quality. The optimization involves three main processes: mating selection, reproduction, and survivor selection, which together guide the population toward a better approximation of the Pareto-optimal set.

One well-known algorithm is Two_Arch2 [3], illustrated in figure below. This algorithm stands out because it maintains two separate archives through its evolutionary process: the convergence archive (CA), which enhances the population's progress toward the Pareto front in terms of convergence, and the diversity archive (DA), which promotes diversity within the population to avoid local optima. More details about Two_Arch2 can be found in [3].

1.3 Procedural Content Generation

Procedural content generation (PCG) often involves multi-objective optimisation challenges [4], [5], such as balancing desired characteristics in game levels, like emptiness [6], [7], and spatial diversity [8], [9]. Moreover, the well-defined problem and the visually understandable solutions make PCG an ideal testbed for elucidating the mechanisms of MOEAs.

2. Sokoban Level Generation

In this section, we introduce the mechanics and level design principles of the game Sokoban, where the player's objective is to push boxes to designated locations, and explored advanced level generation strategies that optimize for emptiness and spatial diversity.

2.1 Sokoban Game Overview

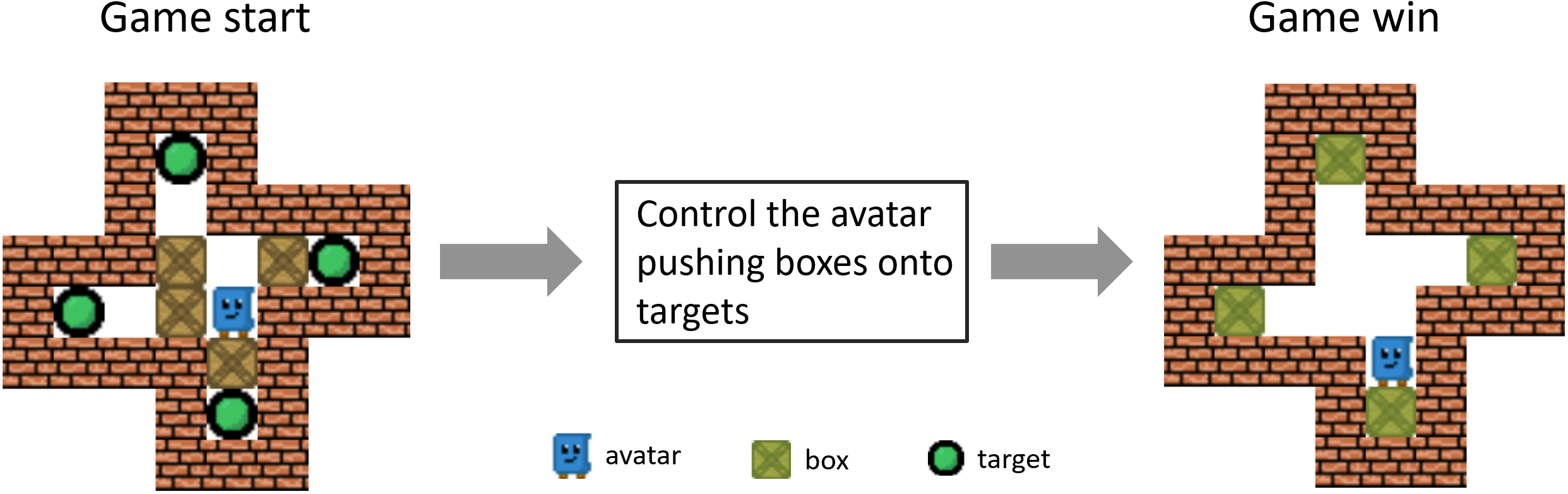
The game layout, start state, and winning state is illustrated in figure below. The layout is designed by Zhao et al., readers who are also interested in MCTS applications in games please refer to [10].

• Goal: The player's goal is to push all the boxes to designated storage locations, clearly marked on the game floor.
• Movement: The player can move the character up, down, left, and right, but can only push boxes, not pull them.
• Restrictions: Each box can only be moved one at a time and cannot be pushed into other boxes or walls, nor through them.
• Level Design: The game is designed like a warehouse with walls that create challenging obstacles. The player starts at a predetermined position and must strategically move the boxes to avoid blocking paths irreversibly.
• Winning Condition: A level is considered passed when all boxes are successfully placed on the goals. Solving the puzzles often requires a minimum number of moves, adding to the challenge.
• Failure Conditions: The game ends in failure if a box is positioned where it cannot be moved further, such as in a corner away from a goal. In such cases, the player must restart the level or undo previous moves to proceed.

2.2 Level Design and Generation Objectives

Following insights from Li et al.'s survey on diversity in game design [6], we focus on spatial diversity and emptiness. These dimensions of diversity enhance the gameplay experience by ensuring that each playthrough remains engaging and unique. Our approach considers various gameplay aspects and player interactions, enriching the gaming experience by offering a variety of challenging scenarios.

We aim to optimize Sokoban levels based on two primary metrics:

1. Emptiness [7]: The percentage of empty tiles in a level, representing how minimalistic a level is.
2. Spatial Diversity [9]: The entropy of the level, representing how different each row in a level is.

\(maximize\) \( \{ f_{\text{emp}}(\text{level}), f_{\text{div}}(\text{level}) \}\),

where \( f_{\text{emp}} \) measures the proportion of empty tiles in a level, promoting minimalism, and \( f_{\text{div}} \), defined as \( -\frac{1}{\log n} \sum_{i=1}^{n} \frac{\alpha p_i}{n} \log \frac{\alpha p_i}{n} \), assesses spatial diversity with values from 0 to 1. A level is segmented into \(n\) parts, with each row representing a segment. \(p_i\) denotes the proportion of empty spaces within each segment, and \(\alpha\) is a normalisation factor, ensuring that \(\sum_{i=1}^{n}\alpha p_i=1\). A higher \( f_{\text{div}} \) indicates greater spatial diversity within a level, while a higher \( f_{\text{emp}} \) suggests the level is more minimalistic.

Playability, another crucial objective in game design, achieved by designing a navigable path in each level that connects the avatar, boxes, and targets. This unobstructed pathway ensures a player path for level functionality and is not encoded as a gene in the chromosome in the MOEA. Additionally, an A* solver tests each level's playability[11] , confirming that all levels displayed are indeed playable.

2.3 Level Setups and its Representation

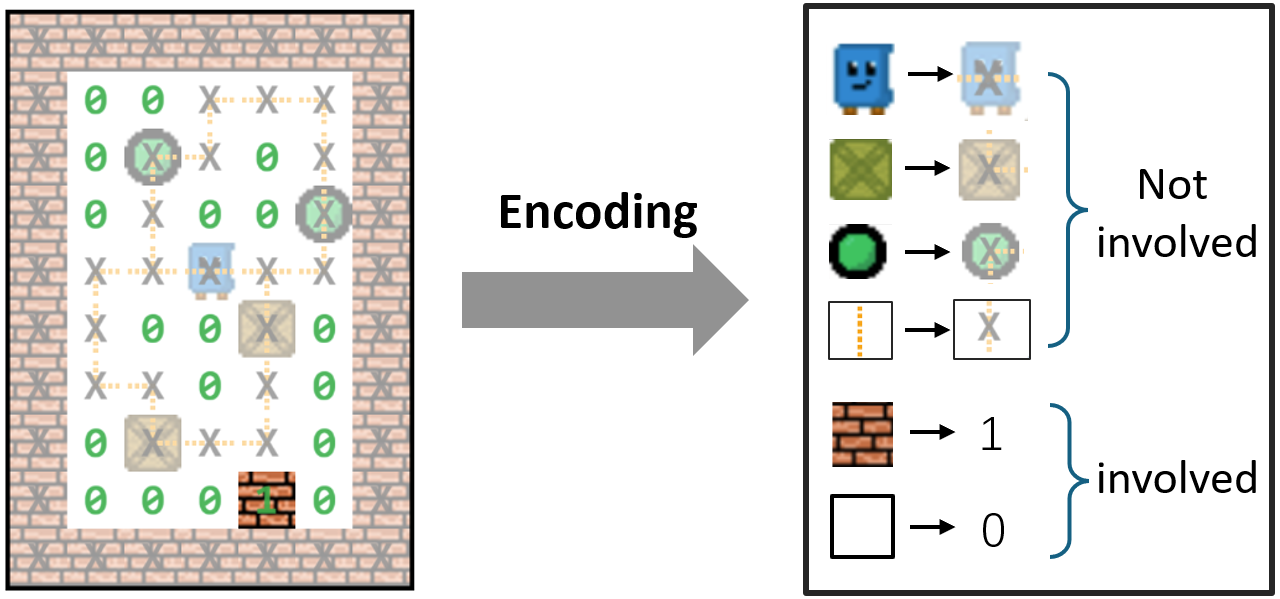
In this section, users can customize the level structure and layouts by inputting numbers, as shown below. The representation of this level is presented on the right by clicking "Generate". Each tile involved in the encoding process is a gene in the chromosome.

Instruction

Instruction

3. Modules Of MOEA

This section offers a detailed walkthrough of Two_Arch2, a well-known multi-objective evolutionary algorithm. Our aim is to decompose the complex processes of Two_Arch2 which can effectively balance convergence and diversity during optimization. The following sections will cover this dual-archive strategy that Two_Arch2 employs, consisting of a CA and a DA, both important for optimal algorithm performance. Key components of the algorithm, mating selection, reproduction, and survivor selection (update CA & DA), will be explored in depth to illustrate their roles in enhancing optimization results.

3.1 Mating Selection

The aim of mating selection is to differentiate and select promising individuals as parents based on their fitness to generate new offspring individuals through reproduction strategy. The reproduction strategy often involves crossover and mutation.

• Crossover involves combining chromosome from two or more parent to produce new chromosome. This process mimics biological reproduction, where traits from different parents are combined to create chromosome with potentially better characteristics.
• Mutation introduces random changes to individual chromosome. It adds diversity to the population by altering the gene of solutions. This randomness prevents the algorithm from getting stuck in local optima.

The process involves a probabilistic approach, where individuals with higher fitness have a greater likelihood of being chosen as parents. Additionally, the mating selection characteristic of the Two_Arch2 algorithm involves strategic pairing of individuals from the CA and the DA. This pairing is designed to balance the exploration and exploitation in the search space by combining individuals with high convergence properties from the CA with those offering greater diversity from the DA.

3.1.1 Crossover Parent Selection

In Two_Arch2, the parent selection for crossover follows a simple yet effective framework, consistent with general MOEAs. The solution set, which includes non-dominated solutions, is divided into two distinct archives: the CA and the DA. These two archives collectively form the parent population for the reproduction phase, which includes both crossover and mutation processes.

Unlike some other MOEAs, Two_Arch2 does not employ a specialized mechanism for selecting parents for crossover. Instead, parents are chosen from the combined pool of CA and DA, leveraging both their convergence and diversity characteristics. After crossover, the resulting offspring are used to update both archives based on their dominance properties, improving the overall solution set by reinforcing both convergence and diversity.

<<

>>

3.1.2 Mutation Parent Selection

The mutation process in Two_Arch2 similarly utilizes the union of CA and DA as a source for parent selection as well. This approach ensures that the mutation phase benefits from a diverse and high-quality set of genetic materials. Parents for mutation are selected based on their ability to contribute to an enriched genetic diversity. The offspring produced through mutation are assessed for their non-dominance; those that do not dominate any existing solutions in either archive are specifically added to the DA to maintain diversity, while dominant offspring update the CA, enhancing the algorithm’s convergence toward optimal solutions.

<<

>>

3.2 Reproduction

The reproduction process in the Two_Arch2 algorithm is a collaborated operation combining crossover and mutation to generate offspring. Crossover starts with a single-point method, randomly exchanging parts of two parent chromosomes to produce varied offspring layouts. In the mutation, a chromosome is altered to further increase diversity, such as switching a wall tile to a floor tile or vice versa. These methods work together to evolve the population towards increasingly optimized game levels, ensuring a balance between difficulty and solvability.

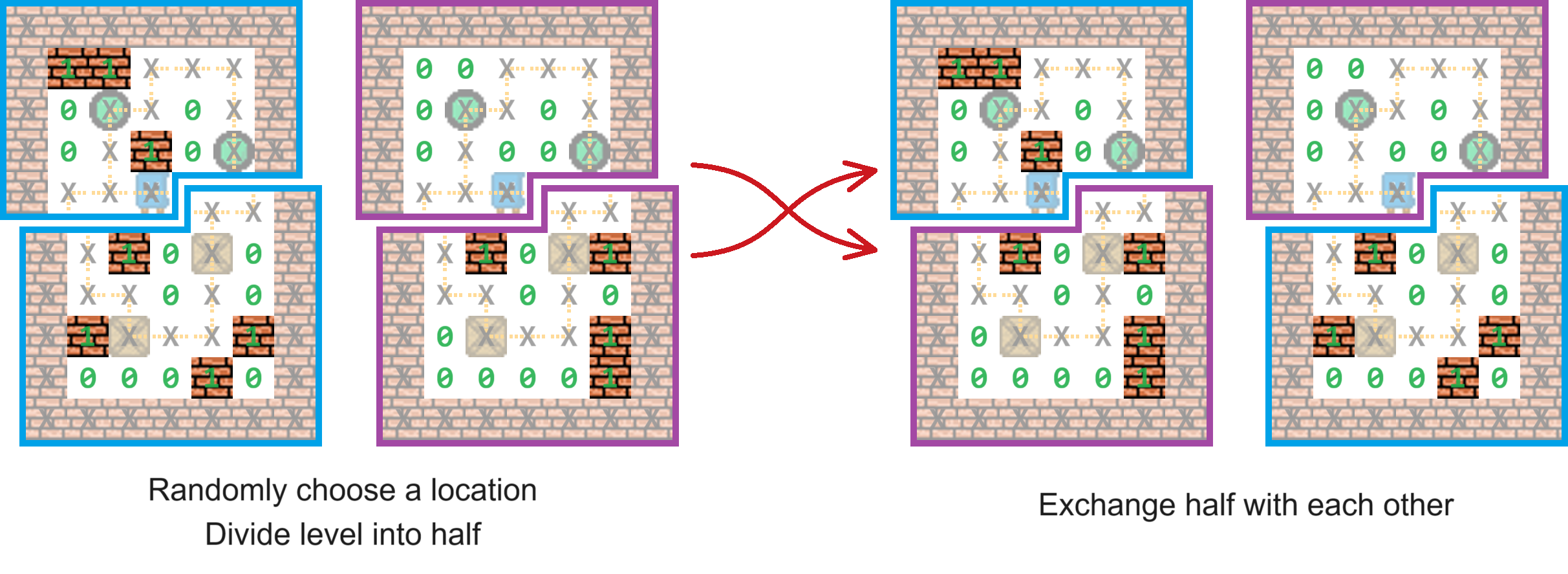
3.2.1 Crossover

In the Two_Arch2 algorithm, the crossover operation plays a crucial role in generating new solutions by combining features from two parent individuals. Each parent possesses a unique level layout, and the crossover is visually illustrated as follows:

A random location within the level layout is selected as the crossover point, effectively splitting each level into two distinct halves. The halves are then exchanged between the two parents (from CA and DA). For example, the top half of the first parent's level might be combined with the bottom half of the second parent’s level, and vice versa. This exchange results in offspring that inherit mixed attributes from both parents, enhancing genetic diversity. The process aims to introduce potentially advantageous traits into new levels, driving the evolutionary progress.

These offspring are then evaluated and sorted into either the CA or the DA, based on their performance and diversity characteristics. The CA focuses on enhancing solution quality by prioritizing offspring that better converge toward optimal solutions. In contrast, the DA is designed to maintain and increase the genetic diversity within the population, ensuring a wide exploration of the solution space. By strategically updating these archives with new offspring, Two_Arch2 continually balances convergence and diversity, optimizing the evolutionary process.

<<

>>

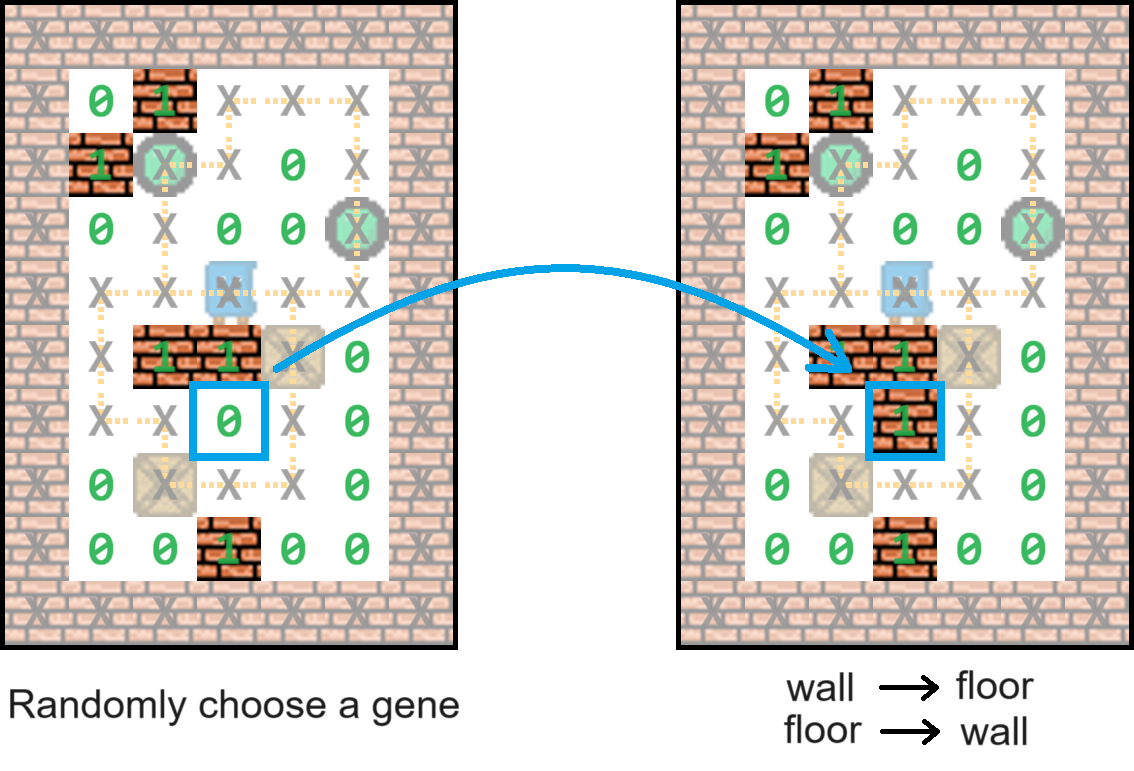
3.2.2 Mutation

In the Two_Arch2 reproduction process, mutation plays a role in introducing variation into the offspring, which helps maintain genetic diversity within the population: A gene is randomly selected within the chromosome representing a level layout. This gene undergoes a mutation, which in the context of a game level, typically means altering the tile type at the corresponding location in the level layout. If the original gene represented a wall (1), it is mutated to become a floor (0), or vice versa.

<<

>>

3.3 Survival Selection

Survival selection is a critical component of the Two_Arch2 algorithm, responsible for determining which individuals will continue on to the next generation. This phase of the algorithm evaluates the offspring generated by the reproduction process against the existing population. It prioritizes the individuals based on their fitness and alignment with the algorithm's objectives.

3.3.1 Update CA

Convergence: Individuals that are closer to the Pareto front are favored. The CA stores these individuals, which represent solutions that are closer to the optimal set of objectives. The CA is thus focused on retaining individuals that demonstrate better objective function values.

<<

>>

3.3.2 Update DA

Diversity: Individuals that contribute to the genetic diversity of the population are also important. The DA captures these varied individuals, ensuring that the population explores a broad search space. The DA helps to prevent premature convergence to suboptimal solutions by preserving a variety of genetic material.

<<

>>

4. Overall Process

The Two_Arch2 algorithm is an evolutionary optimization strategy that systematically evolves a population of solutions through a series of steps designed to both explore and exploit the search space. The whole process can be illustrated below. By iterating through these steps, the Two_Arch2 algorithm ensures the continuous improvement of game levels, balancing between challenging yet solvable puzzles and maintaining diverse level designs to avoid stagnation and promote innovation in gameplay experiences.

<<

>>

6. Conclusion

In conclusion, this immersive exploration into the application of multi-objective evolutionary algorithms (MOEAs) through Sokoban level generation provides a comprehensive understanding of how MOEAs can be leveraged to enhance game levels. By integrating concepts such as mating selection, reproduction, and survival selection, the Two_Arch2 algorithm demonstrates its efficacy in balancing convergence and diversity, thus optimizing the procedural generation of game levels. This collaboration not only underscores the potential of MOEAs in PCG applications but also showcases their practical implementation in creating diverse, stylized, and challenging gaming experiences.