Playing with Monte-Carlo Tree Search

I. Introduction

Monte-Carlo Tree Search (MCTS) is a tree-based policy that aims to achieve optimal performance for sequential decision problems [1], in which actions taken by an agent not only affect the current outcome, but also have a long-term effect. MCTS leverages the concept of tree search to address situations where local optimal actions may not lead to global optimal performance. Because of its simplicity and few requirements for domain knowledge, MCTS has been widely used and achieved significant success for these problems, such as Go [2], video games [3], and chemical synthesis [4].

MCTS leverages the concept of tree search to address situations where local optimal actions may not lead to global optimal performance. The four core components of MCTS are Selection, Expansion, Simulation, and Backpropagation. The basic procedure of MCTS involves building a tree with nodes that represent visited states and selecting the node with the highest probability of reaching an optimal outcome. The selected node is then expanded according to the available action space. Once a simulation terminates, the results of the simulation are propagated back to update the statistics of the nodes on the trajectory. A game tree is then constructed to identify the optimal action at each state. MCTS addresses the exploration-exploitation dilemma with specific selection strategies such as the upper confidence bound (UCB) [5] that balance exploitation and exploration within a given computational budget.

II. Games

Two classic two-player board games, Tic-Tac-Toe and Go, and a single-player video game, Sokoban, are used as immersive examples to examine the abilities of MCTS in different cases such as opponent modeling and deep exploration. Screenshots of the three games are illustrated in Figure 1.

Figure 1:
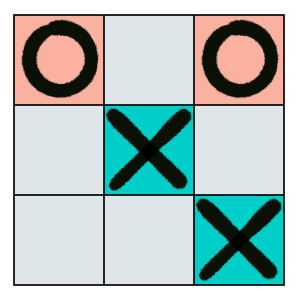
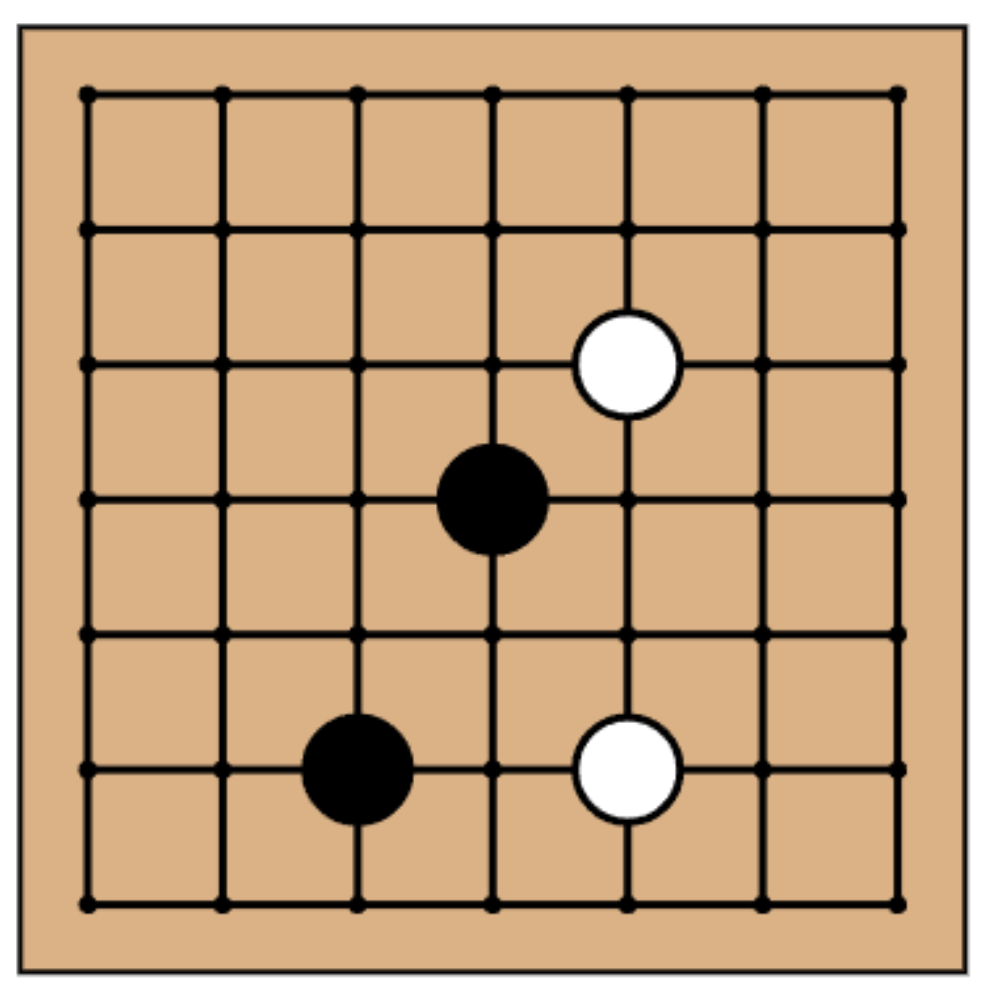
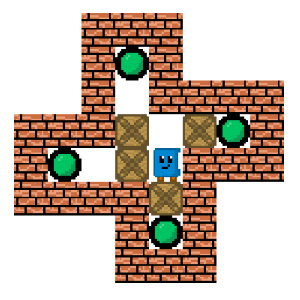
Tic-Tac-Toe (left), Go (center), and Sokoban (right)

• Tic-Tac-Toe is a two-player competitive board game with a limited length of a gameplay. Players take turns drawing their own marker (usually “X” or “O”) on a $3\times3$ grid board, as presented in Figure 1 (left). A player wins once three markers the individual places can be connected together vertically, horizontally, or diagonally. However, if all squares are filled but neither player has won, the game ends in a draw. Due to the participation of the counterpart, MCTS is involved with the min-max and opponent modeling problem.
• Go is a two-player competitive board game, as illustrated in Figure 1 (center), in which two players take turns placing black and white stones on the board. The game begins with an empty board controlled by the player holding black stones. If a player's stones manage to encircle the opponent's stones, then the surrounded stones are removed from the board. The objective of Go is to control more area on the board than the opponent by strategically placing stones. A $7 \times 7$ board is used as the interactive example in this immersive article, following the Tromp-Taylor rules [6], which calculate a player's score by adding the number of stones of its color and the number of empty points that are only connected to stones of its color.
• Sokoban is a one-player puzzle game in which a player must strategically push boxes to their designated positions to win. The game is set on a fixed board made up of different tiles, as demonstrated in Figure 1 (right). The player can move through empty spaces and push boxes to spaces without obstacles like walls and other fixed boxes. In this game, the representation of the state is more complex than Tic-Tac-Toe, and a challenge of deep exploration with unlimited steps arises.

III. Algorithm

Modeling

MCTS is typically used to solve sequential decision problems, which are often formulated as a Markov decision process (MDP). The four components of an MDP are state $S$, action $A$, transition model $P$, and reward $R$. An MCTS policy $\pi$ takes an action in a given state $s$ and obtains a reward $r$ and the next state $s'$ according to the transition model, aiming at maximizing the long-term expected reward. For example, in Tic-Tac-Toe, as shown in Figure 1 (left), state of the game is the game board, represented as nodes in the game tree. The marker placed by a player is considered an action taken by that player.

The interactive interface is implemented based on [7]. The game interfaces and data representations of Tic-Tac-Toe and Sokoban are presented below. You can activate either game by hovering your mouse pointer over its corresponding image.

In Tic-Tac-Toe, the game state is represented as a $3 \times 3$ matrix. The below panel presents the current state of the Tic-Tac-Toe game, where empty spaces indicate unoccupied cells. Human's pieces and those of the AI are denoted by “1” and “-1”, respectively.

Similar to Tic-Tac-Toe, Go shares a similar representation structure with a $7 \times 7$ matrix. The digit “1” represents a white stone, while “-1” represents a black stone. Empty spaces are represented by “0”. The small colored rectangle on the board indicates the “territory” controlled by white stones or black stones.

The Sokoban game is represented by an $n \times n$ matrix, where $n$ represents the size of the game board. The matrix uses “0”, “1”, “2”, “3”, and “4” to indicate empty spaces, walls, boxes, targets, and the player, respectively.

Figure 5:
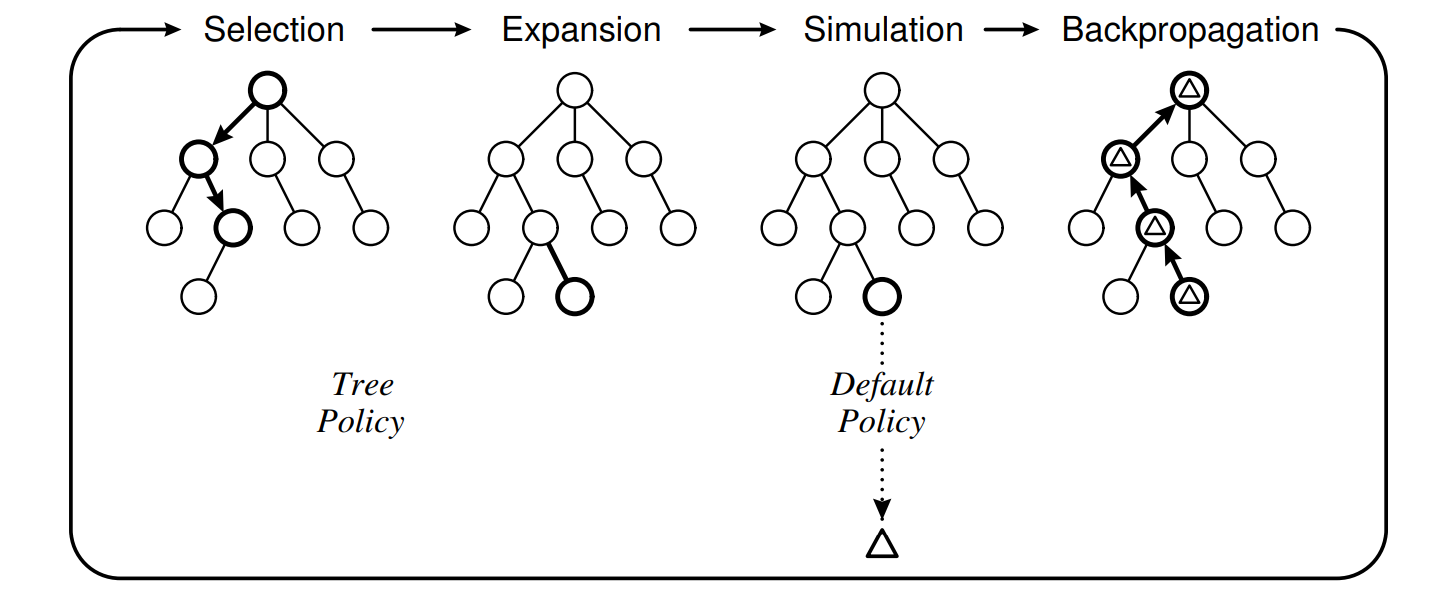
Main steps of MCTS (Figure 2 from [1] ). Nodes and branches represent state and action, respectively. Wins and visit counts are usually the values of a node.

The MCTS follows a workflow, as illustrated in Figure 5, and involves four main components: Selection, Expansion, Simulation, and Backpropagation. The specific four steps will be presented in detail in the subsequent sections. Interactive components are provided to demonstrate these steps intuitively.

Selection

From the root node, which typically represents the current state (e.g., a game board), a specific traversal strategy is applied to navigate the tree and identify the final node. This node is chosen based on its high likelihood to an optimal solution, as determined by the selection strategy. However, the lack of exploration may result in ignoring a better solution. This is known as the “exploration-exploitation dilemma” that MCTS encounters. The dilemma considers a general problem of choosing actions that seem to be optimal at current state or exploring some actions that have not or have only rarely been sampled before. Three commonly used selection strategies are described as follows.

• A random strategy selects nodes randomly.
• The $\epsilon$-greedy strategy selects nodes randomly with probability $\epsilon$, or otherwise, selects the node that has the highest reward with probability $1-\epsilon$.
• The upper confidence bound (UCB) [5] measures the uncertainty of the expected reward of an action. Formula of UCB is $$ UCB = x_i +c\sqrt{\frac{\ln{n}}{n_i}} \qquad (1)$$ in which $\bar{x}_i$ is the averaged return of selecting the action $i$, $n$ denotes the visit counts of the current node, $n_i$ is the number of counts that the action $i$ is selected, and $c$ is the exploration factor. The next child node with the highest UCB value will be selected. UCB is the most commonly used selection strategy in MCTS, called UCB for trees (UCT). It balances the exploration and exploitation by considering both reward and visit counts of a node. $x_i$ estimates the current collected experience, while $c\sqrt{\frac{\ln{n}}{n_i}}$ considers the visit frequency, in which $c$ controls the importance of exploration. Less frequently visited nodes will be chosen with higher possibilities. Hence, unknown areas will be explored more frequently.

The procedure of Selection is shown below.

              \begin{algorithm}
              \caption{Selection}
              \begin{algorithmic}
              \PROCEDURE{Select}{$root$}
              \STATE Set $node$ $\gets$ $root$
              \WHILE {$node$ is not leaf and $node$ is not fully explored}
              \STATE $node$ $\gets$ Node with the highest UCB value (Eq. (1)) among $node.children$
              \ENDWHILE
              \STATE \Return $node$
              \ENDPROCEDURE
              \end{algorithmic}
              \end{algorithm}
            

You can try out the Selection procedure in the interactive panel below.

Expansion

Expansion explores new states and adds new nodes to the tree. A node is expandable if it has remaining available actions. Once a node is selected, the algorithm expands by adding new child nodes according to the available actions. If the node chosen by Selection procedure has no available action, other paths will be explored to find an expandable node. The number of expanded nodes usually depends on the available actions and computation budget.

The procedure of Expansion is shown as follows.

              \begin{algorithm}
              \caption{Expansion}
              \begin{algorithmic}
              \PROCEDURE{Expand}{node}
              \STATE Sample $a$ from unvisited actions of $node$
              \STATE $new\_node$ $\gets$ $node$ after taking action $a$
              \STATE $node.children.append(new\_node)$
              \STATE \Return $new\_node$
              \ENDPROCEDURE
              \end{algorithmic}
              \end{algorithm}
            

You can test the procedure of Expansion in the interactive panel below.

Simulation

Starting from the expanded node, the roll-out strategy is conducted to simulate a gameplay. The choice of simulation policy has a large impact on the final result. A common strategy for selecting actions is to use a random policy for its simplicity, which chooses actions uniformly at random at successive states. The simulation step repeats until a terminal state is reached. The results of the simulation, such as the final state or a reward value, are then collected and used to update the values of the node. A major concern for the policy is the efficiency issues. Some improved ingredients have been made, such as rule-based simulation and learning methods [4] [8] .

The procedure of Simulation is shown as follows.

              \begin{algorithm}
              \caption{Simulation}
              \begin{algorithmic}
              \PROCEDURE{Simulate}{node}
              \STATE $r \gets 0$
              \While{not terminated}
                \STATE Sample $a$ from available actions of $node$
                \STATE $new\_node$ $\gets$ $node$ after taking action $a$
                \STATE $r \gets r+evaluate(new\_node)$
                \STATE $node$ $\gets$ $new\_node$
              \ENDWHILE
              \STATE \Return $r$
              \ENDPROCEDURE
              \end{algorithmic}
              \end{algorithm}
            

You can try out the Simulation procedure in the interactive panel below.

Backpropagation

Statistics will be propagated back along the visited path of the expanded node after simulation. The visit counts and values, such as reward and wins of all nodes in the path upon the expandable node, will be updated according to the results of the simulation. Considering Tic-Tac-Toe, players A and B make moves in turn. To determine the next move for player A, MCTS obtains the action that leads to win with the highest possibility in current state. Nodes represent game states in the tree, and each layer corresponds to a player. Thus, the expandable states belong to player B, i.e., those where B would take a next move. If, after simulating a number of future moves, it is determined that A wins the game, then the result of the game is propagated back along with the trajectory. It is notable that since Tic-Tac-Toe is a two-player competitive game, the value update mechanism of nodes is different compared to the single-player case. For example, wins for nodes that belong to A will be incremented by one, while wins for B's nodes will be decremented. All updates are limited to nodes that trace back from the expanded node in the simulation. During the backpropagation phase of MCTS, the statistics gathered during Simulation are propagated back along the path up the tree from the expanded node. This involves updating the visit counts and values like rewards and wins, for all nodes along the path from the expanded node to the root node of the tree. Considering Tic-Tac-Toe, players A and B take turns making moves. When MCTS determines the next move for player A, it obtains the action that leads to win with the highest probability in the current state. The tree is built with different layers representing the players, so the expandable states belong to player B, i.e., those where B would move next. If, after simulating a number of future moves, it is determined that A wins the game, the visit count for each of the nodes in the visited path will be incremented by one. It is notable that since Tic-Tac-Toe is a two-player competitive game, the value update mechanism of nodes is different compared with the single-player case. For example, wins for nodes that belong to player A will be incremented by one, while wins for nodes that belong to player B will be decremented, if player A wins the game according to the Simulation. All updates are limited to nodes that trace back from the expanded node for the Simulation.

The procedure of Backpropagation is shown as follows.

              \begin{algorithm}
              \caption{Backpropagation}
              \begin{algorithmic}
              \PROCEDURE{Backpropagation}{$node$, $value$}

                \STATE $node.visit$ $\gets$ $node.visit+1$

                \IF{node is root}
                  \RETURN
                \ENDIF

                \STATE $node.value$ $\gets$ $node.value+value$
                \STATE Backpropagation(node.parent, value)

              \ENDPROCEDURE
              \end{algorithmic}
              \end{algorithm}
            

You can test the backpropagation in the interactive panel below.

By integrating the four essential components of Selection, Expansion, Simulation, and Backpropagation, a succinct and cohesive algorithm for the complete MCTS process can be constructed. Finally, the child node with the highest visit count is selected as the best move, since it has been selected and evaluated more often during the tree growth, which may result in a robust performance.

              \begin{algorithm}
              \caption{MCTS}
              \begin{algorithmic}
              \PROCEDURE{Mcts}{root}
              \While{not end\_condition}
                \State $node$ $\gets$ Select($root$)
                \State $node$ $\gets$ Expand($node$)
                \State $value$ $\gets$ Simulate($node$)
                \State Backpropagation($node$, $value$)
              \EndWhile
              \Return Highest visit value node in $root.children$
              \EndProcedure
              \end{algorithmic}
              \end{algorithm}
            

An example of a good move

IV. Practice

MCTS is a powerful algorithm that can effectively handle various types of games, including adversarial games like Tic-Tac-Toe and Go, as well as puzzle games such as Sokoban. In the following sections, we will delve into how MCTS works in these three games and provide interactive components to illustrate its effectiveness.

For the Tic-Tac-Toe game, choose “Human” or “AI” to decide who goes first. During the player's turn, click on the highlighted area on the board to make a move. During the AI player's turn, you can select one of three decision-making modes for the AI player: random, greedy, and MCTS. In MCTS, you can move the slider to select the number of iterations. The higher the number of iterations is, the better decisions the AI player will make. In the MCTS panel on the right, choose “Next step” to view the steps of MCTS at each stage or select “Next iteration” to see the situation after each iteration, including Selection, Expansion, Simulation, and Backpropagation. The tree displays the current MCTS information. The possible future actions of the opponent are estimated during searching, which is considered as a case of opponent modeling. You can also select “Visualize last step” to directly view the final step and each node's value. Finally, click “Make play” to take AI's action.

In Sokoban, selecting “Auto play” enables the MCTS to run automatically. At each step, the MCTS will select the optimal solution it found. Alternatively, you can use “Make MCTS Move” to view each step of the search in detail on the right panel. You can also choose to play manually by moving the mouse to the game and using W, A, S, D or arrow keys to move.

An interactive example of Go is shown below. We choose a $7\times7$ board and follow the Tromp-Taylor rules [6] for MCTS simulations same as Alpha Zero [2]. This is because human rules, such as Chinese rules, can not be clearly implemented to a machine language that is resulted from the need to reach an agreement on dead stone removal issues. The lack of dead stone removal when the game terminates makes Tromp-Taylor rule much easier to write Go simulator for MCTS. AI researchers can devote more time and effort to the research through Tromp-Taylor rules instead of learning complex and ambiguous rules for months. The goal of this game is to cover more area than the opponent. The AI player can choose to play randomly or use the MCTS algorithm to make its moves. During the construction of the search tree, the AI player takes into account opponent modeling, estimating the potential effects of the opponent's decisions on the progression of the game.

V. Conclusion

In summary, this paper provides a comprehensive explanation of the basic procedure of MCTS. Four main components, Selection, Expansion, Simulation, and Backpropagation are described in detail. To fully demonstrate the workflow of MCTS in two-player and single-player cases, three classic games, Tic-Tac-Toe, Go, and Sokoban are used. MCTS has been successfully applied to game AI areas such as Go [2] and video games [3]. Beyond these game-based environments, MCTS also presents its abilities in black-box optimization [9], robotics [10], and real-world scheduling problems [11]. Readers are referred to [1,2] for more about MCTS, its variants, and applications.